Comprensión de las matemáticas detrás del método de impurezas de Gini para la división del árbol de decisión

Estás leyendo la publicación: Comprensión de las matemáticas detrás del método de impurezas de Gini para la división del árbol de decisión

La impureza de Gini es una función que determina qué tan bien se dividió un árbol de decisión. Básicamente, nos ayuda a determinar qué divisor es el mejor para que podamos construir un árbol de decisión puro. La impureza de Gini oscila entre los valores de 0 a 0,5. Es uno de los métodos para seleccionar el mejor divisor; otro método famoso es la Entropía, que varía de 0 a 1. En este artículo, veremos el concepto matemático del método de impurezas de Gini para la división del árbol de decisión. Tomaremos datos aleatorios y entenderemos este concepto desde lo básico. A continuación se muestra una lista de puntos que cubriremos en este artículo.

Tabla de contenido

1. ¿Qué es un árbol de decisión?
2. Las matemáticas detrás de la impureza de Gini
3. Construyendo el árbol de decisión usando la impureza de Gini

Comencemos con una introducción rápida a los árboles de decisión.

¿Qué es un árbol de decisión?

Un árbol de decisión es el algoritmo de aprendizaje automático supervisado. Como su nombre indica, si lo visualizamos, aparecerá como un árbol. Es un algoritmo poderoso que puede funcionar bien en datos complejos, también es de naturaleza versátil porque puede realizar clasificación y regresión.

Los árboles de decisión tienen un nodo raíz, nodos internos y nodos hoja donde,

1. Nodo raíz: Es un nodo desde donde se origina el árbol.
2. Nodos internos: este nodo contiene la única evaluación de variables
3. Nodos hoja: estos nodos son los encargados de tomar decisiones

Ahora, repasaremos las matemáticas detrás de la impureza de Gini implementando un árbol de decisiones en un conjunto de datos determinado.

Las matemáticas detrás de la impureza de Gini

Echemos un vistazo a la fórmula de la impureza de Gini. La fórmula de la impureza de Gini se da como:

Dónde,

El j representa el número de clases en la etiqueta, y

El PAG representa la relación de clase en el i-ésimo nodo.

La impureza de Gini tiene un valor máximo de 0,5, que es lo peor que podemos obtener, y un valor mínimo de 0 significa lo mejor que podemos obtener.

Construyendo el árbol de decisión usando la impureza de Gini

Usaremos el conjunto de datos de billetes para implementar un árbol de decisiones. El conjunto de datos comprende los detalles de si un billete es auténtico o no. Se dan dos características y la etiqueta tiene dos valores 0 o 1. (0 para auténtico, 1 para no auténtico).

Hemos tomado solo 10 filas como muestra para facilitar el trazado de un árbol y una mejor comprensión de la impureza de Gini.

Construyamos el árbol de decisión para los datos dados. Para cada valor de características, calculamos la impureza de Gini ya que nuestra característica es continua. No es factible calcular cada valor uno por uno, por lo que tomaremos un valor para cada característica.

Ahora, calcularemos las puntuaciones de impurezas de Gini para las diferentes combinaciones de valores de cada una de las variables.

Varianza de Wavelet

Para valores <= 0,9, tenemos 8 registros de 10 y 2 registros con valores> 0,90.

• Para Varianza de Wavelet <=0,9 y clase == 1 los valores son 6, por lo que la relación será 6/8
• Para Varianza de Wavelet <=0,9 y clase == 0 los valores son 2, por lo que la relación será 2/8
  • Gini = 1 – ((6/8)^2 + (2/8)^2) = 0.38 (usando la fórmula anterior)

• Para Varianza de Wavelet >0.9 y clase == 0 los valores son por lo que la relación será 2/2
• Para Varianza de Wavelet >0.9 y clase == 1 los valores son por lo que la relación será 0/2
  • Gini = 1 – ((2/2)^2 + (0/2)^2) =

Gini = 0 significa que es el nodo más puro y es una hoja.

Sesgo de wavelet

Para valores <= 7.161, tenemos 7 registros de 10 y 3 registros con valor >7.161.

• Para Sesgo de wavelet <=7.161 y clase == 0 los valores son 1 por lo que la relación será 1/7
• Para Sesgo de wavelet <=7.161 y clase == 1 los valores son 6, por lo que la relación será 6/7
  • Gini = 1 – ((1/7)^2 + (6/7)^2) = 0,25

• Para Sesgo de wavelet >7.161 y clase == 0 los valores son 3 por lo que la relación será 1/3
• Para Sesgo de wavelet >7.161 y clase == 1 los valores son 0 por lo que la relación será 0/3
  • Gini = 1 – ((1/3)^2 + (0)^2) = 0

Gini = 0 significa que es el nodo más puro y es una hoja.

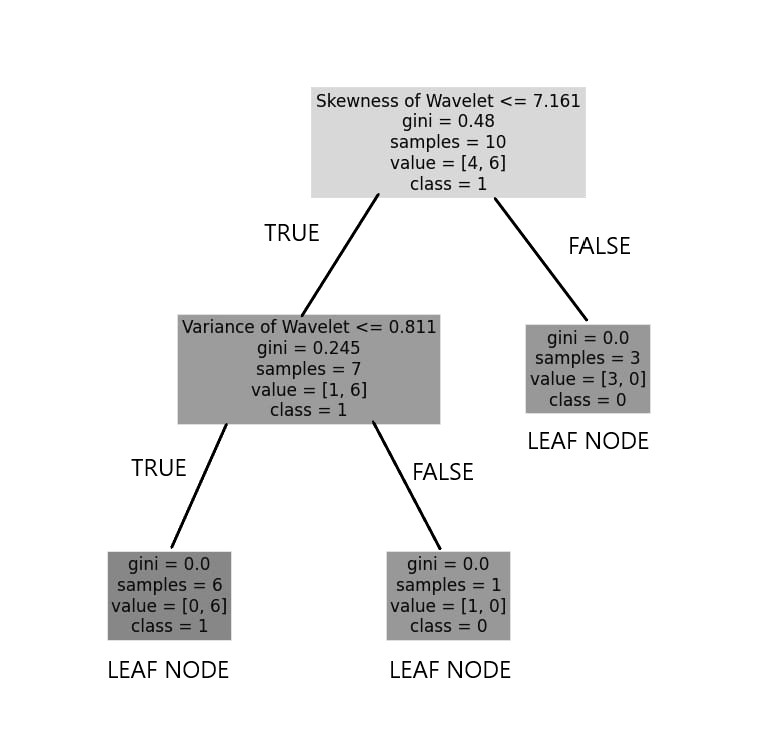
tomaremos el Sesgo de la wavelet como el nodo raíz porque tiene menor impureza que el Varianza de la wavelet. Después de calcular los valores anteriores, obtenemos este árbol de decisión como:

Árbol de decisión

Podemos ver el nodo raíz como el sesgo de la wavelet. Tiene un total de 10 muestras y de las cuales ‘0’ son 4 y ‘1’ son 6, y está etiquetado como clase 1 porque la mayoría de los valores de clase son 1, por eso, dado que no es un nodo hoja, entonces no podemos tomar una decisión. Para la condición <=7.161 FALSE( > 7.161) como resultado, obtenemos el nodo hoja que tiene GINI = 0; lo que significa que es el nodo más puro que no se puede dividir más.

Para la condición <=7.161 TRUE hemos calculado GINI = 0.2579 pero por el valor de Variance of wavelet <= 0.811 funciona mejor que Skewness of wavelet. Es por eso que calculamos la asimetría de la wavelet en lugar de la varianza de la wavelet. Las funciones se pueden repetir y no se pueden repetir.

Ahora calcularemos la impunidad de Gini para el nodo izquierdo del nodo raíz.

Varianza de Wavelet

Para valores <= 0,811, tenemos 6 registros de 7 y 1 registro con valores> 0,811.

• Para Varianza de Wavelet <=0,811 y clase == 0 los valores son 0, por lo que la relación será 0/6
• Para Varianza de Wavelet <=0,811 y clase == 1 los valores son 6, por lo que la relación será 6/6
  • Gini = 1 – ((0/7)^2 + (6/6)^2) =

Gini = 0 significa que es el nodo más puro y es una hoja.

• Para Varianza de Wavelet >0.811 y clase == 0 los valores son por lo que la relación será 1/1
• Para Varianza de Wavelet >0.811 y clase == 1 los valores son por lo que la relación será 0/1
  • Gini = 1 – ((1/1)^2 + (0/2)^2) =

Gini = 0 significa que es el nodo más puro y es una hoja.

Arriba, acabamos de calcular los nodos hoja del subárbol izquierdo. Teniendo en cuenta este proceso, el árbol final se vería como,

Ultimas palabras

En este artículo, aprendimos sobre el árbol de decisión e implementamos el árbol de decisión para la clasificación binaria. Para construir un árbol de decisión, usamos el método de impurezas de Gini para dividir el árbol. Podríamos entender el concepto matemático del enfoque en detalle.