Estás leyendo la publicación: Un nuevo enfoque de investigación de inteligencia artificial (IA) presenta el aprendizaje en contexto basado en indicaciones como un problema de aprendizaje de algoritmos desde una perspectiva estadística
Aprendizaje en contexto es un paradigma reciente donde un modelo de lenguaje grande (LLM) observa una instancia de prueba y algunos ejemplos de entrenamiento como su entrada y decodifica directamente la salida sin ninguna actualización de sus parámetros. Este entrenamiento implícito contrasta con el entrenamiento habitual donde se cambian los pesos en base a los ejemplos.
Aquí viene la pregunta de por qué el aprendizaje en contexto sería beneficioso. Puede suponer que tiene dos tareas de regresión que desea modelar, pero la única limitación es que solo puede usar un modelo para ambas tareas. Aquí, el aprendizaje en contexto es útil, ya que puede aprender los algoritmos de regresión por tarea, lo que significa que el modelo utilizará regresiones ajustadas separadas para diferentes conjuntos de entradas.
En el papel “Transformadores como algoritmos: generalización y selección implícita de modelos en el aprendizaje en contexto” han formalizado el problema del aprendizaje en contexto como un problema de aprendizaje de algoritmos. Han utilizado un transformador como algoritmo de aprendizaje que puede especializarse mediante entrenamiento para implementar otro algoritmo objetivo en el momento de la inferencia. En este artículo, exploraron los aspectos estadísticos del aprendizaje en contexto a través de transformadores e hicieron evaluaciones numéricas para verificar las predicciones teóricas.
En este trabajo, han investigado dos escenarios, en el primero los avisos están formados por una secuencia de pares iid (entrada, etiqueta), mientras que en el otro la secuencia es una trayectoria de un sistema dinámico (el siguiente estado depende del estado anterior : Xm+1 = f(xmetro) + ruido).
Ahora viene la pregunta, ¿cómo entrenamos a tal modelo?
En la fase de formación de ICL, T las tareas están asociadas con una distribución de datos {Dt}t=1T. Muestrean secuencias de entrenamiento de forma independiente St de su distribución correspondiente para cada tarea. Luego pasan una subsecuencia de St y un valor X de la secuencia St para hacer una predicción sobre X. Aquí es como el marco de meta-aprendizaje. Después de la predicción, minimizamos la pérdida. La intuición detrás del entrenamiento de ICL puede interpretarse como la búsqueda del algoritmo óptimo para adaptarse a la tarea en cuestión.
Luego, para obtener límites de generalización en ICL, tomaron prestadas algunas condiciones de estabilidad de la literatura sobre estabilidad de algoritmos. En ICL, un ejemplo de entrenamiento en el indicador influye en las decisiones futuras de los algoritmos a partir de ese punto. Entonces, para lidiar con estas perturbaciones de entrada, necesitaban imponer algunas condiciones en la entrada. Puedes leer [paper] para más detalles. Figura 7 muestra los resultados de los experimentos realizados para evaluar la estabilidad del algoritmo de aprendizaje (Transformador aquí).


RMTL es el riesgo (~error) en el aprendizaje multitarea. Una de las ideas del límite derivado es que el error de generalización de ICL se puede eliminar aumentando el tamaño de la muestra norte o el número de secuencias METRO por tarea Los mismos resultados también pueden extenderse a sistemas dinámicos estables.
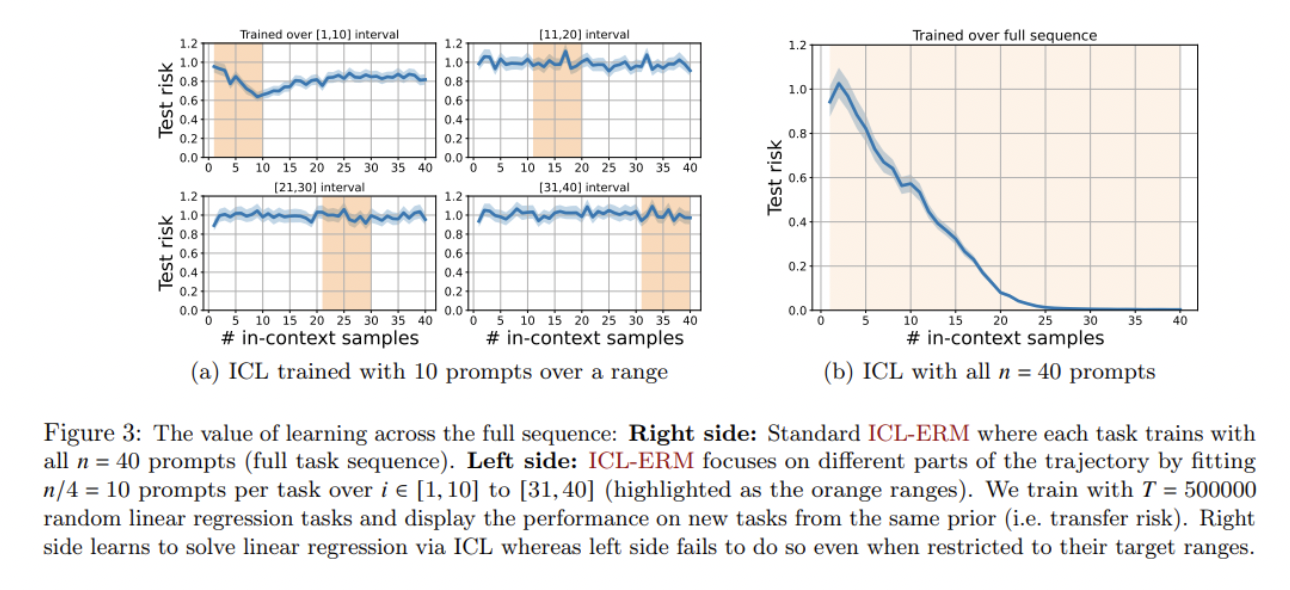

Ahora veamos la verificación de estos límites usando evaluaciones numéricas.
arquitectura GPT-2 que contiene 12 capas, 8 cabezas de atención y se utiliza una incrustación de 256 dimensiones para todos los experimentos. Los experimentos se realizan sobre regresión y dinámica lineal.
- Regresión lineal: En ambas figuras (2(a) y 2(b)), los resultados de aprendizaje en contexto (rojo) superan los resultados de los mínimos cuadrados (verde) y están perfectamente alineados con la solución ponderada/de cresta óptima (puntos negros). Esto, a su vez, proporciona evidencia de la capacidad de selección de modelos automatizados de los transformadores mediante el aprendizaje de tareas previas.
- Sistemas dinámicos parcialmente observados: En las Figuras (2(c) y 6), los resultados muestran que el aprendizaje en contexto supera los resultados de mínimos cuadrados de casi todos los órdenes H=1,2,3,4 (donde H es el tamaño de la ventana que se desliza sobre la secuencia de estado de entrada para generar una entrada al modelo similar a la longitud de la subsecuencia)
En conclusión, demostraron con éxito que los resultados experimentales se alinean con las predicciones teóricas. Y para la dirección futura de los trabajos, valdría la pena explorar varias preguntas interesantes.
(1) Los límites propuestos son para el riesgo MTL. ¿Cómo se pueden controlar los límites de las tareas individuales?
(2) ¿Se pueden extender los mismos resultados de sistemas dinámicos totalmente observados a sistemas dinámicos más generales como el aprendizaje por refuerzo?
(3) De la observación se concluyó que el riesgo de transferencia depende únicamente de las tareas MTL y su complejidad y es independiente de la complejidad del modelo, por lo que sería interesante caracterizar este sesgo inductivo y qué tipo de algoritmo está aprendiendo el transformador. .


